Derivatives have many uses outside of mathematics and everyday life, including in subjects like science, engineering, physics, and others.
You must have mastered the ability to calculate the derivative of various functions in earlier courses, including trigonometric, implicit, logarithm, etc.
d2y/dx2 and (dydx)^2 are two derivative equations. But to understand them, first, you need to understand what exactly is the second derivative.
The derivative of a function in calculus is known as the second derivative, sometimes known as the second-order derivative.
The second derivative, roughly speaking, measures how a quantity’s rate of change is itself changing. For instance, the second derivative of an object’s position with respect to time is the object’s instantaneous acceleration or the rate at which the object’s velocity is changing with respect to time.
In this article, I’ll tell you what the difference is between d2y/dx2=(dy/dx)^2 and what exactly the derivative means.
D2y/dx2 Vs (dy/dx)^2
Derivative of dy/dx (These 2s may look like index notation, but they aren’t). (dy/dx)2, on the other hand, is the square of the first derivative.
Example:
Take Y=3????3+6????2y=3×3+6×2
The first derivative: dy/dx=9????2+12????dydx=9×2+12x
The second derivative: d2yd????2=18????+12d2ydx2=18x+12
The square of the first derivative: (dy/dx)2=(9????2+12????)2=(81????4+216????3+144
What Is the Second Derivative?
When you differentiate the derivative, you get the second derivative. Remember that dy/dx is the derivative of y with respect to x. The second derivative, pronounced “dee two y by d x squared,” is represented as d2y/dx2.
The nature of stationary points can be more easily ascertained using the second derivative (whether they’re maximum points, minimum points, or points of inflection).
When dy/dx = 0, a curve reaches a stationary point. The type of stationary point (maximum, minimum, or point of inflection) can be determined using the second derivative once the location of the stationary point has been established.
| d2y/d2x=Positive | It’s a minimum point |
| d2y/d2x=Negative | It’s a maximum point |
| d2y/d2x Equals to Zero | It’s both a minimum and maximum point |
| d2y/d2x=0 | Test the values of dy/dx on either side of the stationary point, as before in the stationary points section |
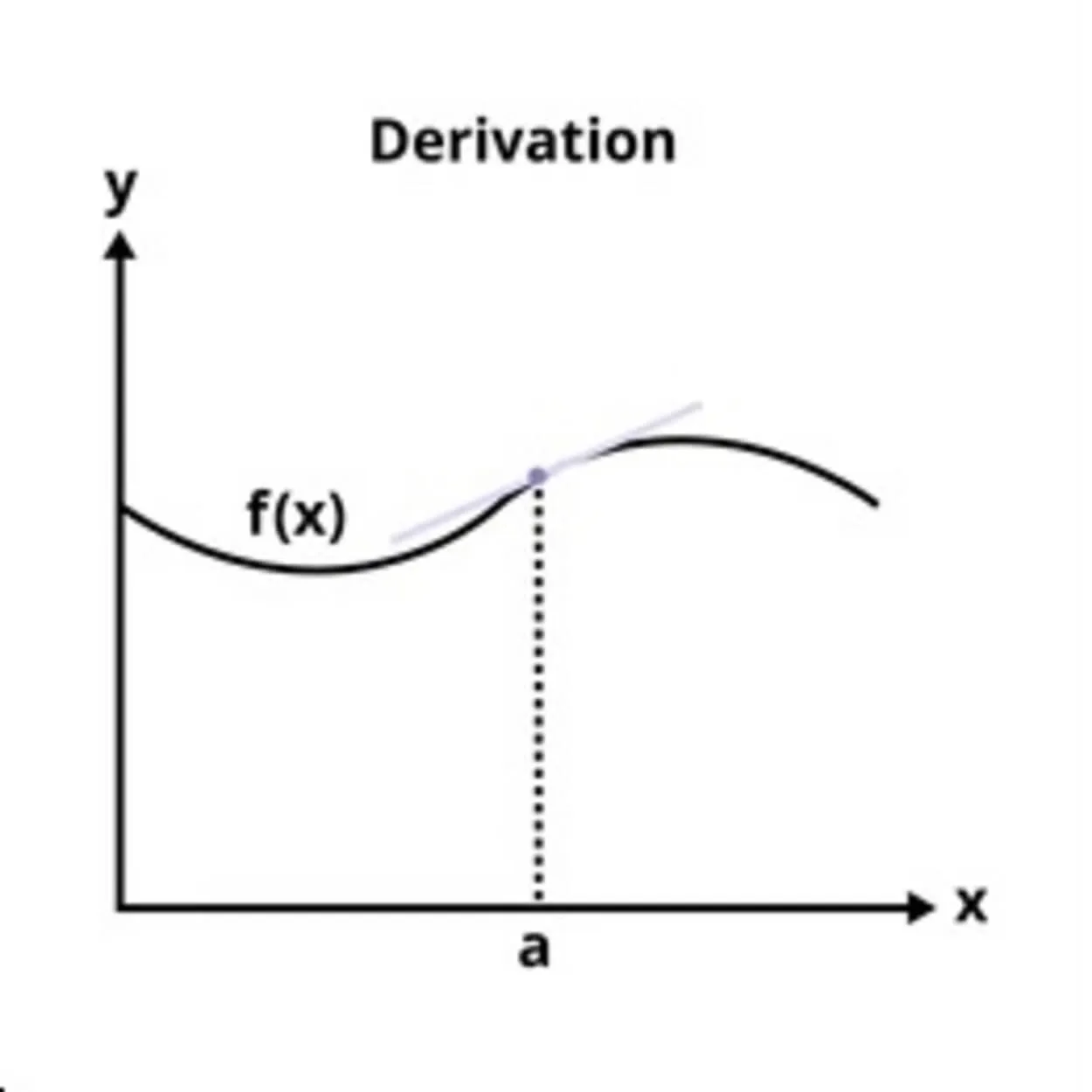
What Is Derivative?
The derivative of a function of a real variable in mathematics quantifies the sensitivity of the function’s value (output value) to changes in its argument (input value). Calculus’s core tool is the derivative.
The velocity of an item, for instance, is the derivative of its position with respect to time. It quantifies how quickly the object’s position varies as time passes.
When it occurs, the slope of the tangent line to the function’s graph at a given input value is the derivative of a function of a single variable. The function closest to that input value is best approximated linearly by the tangent line.
Because of this, the derivative is frequently referred to as the “instantaneous rate of change,” which is the ratio of the instantaneous change in the dependent variable to that in the independent variable.
To include functions of several real variables, derivatives can be generalized. This generalization reinterprets the derivative as a linear transformation whose graph, after a suitable translation, is the best linear approximation to the graph of the original function.
Regarding the foundation provided by the selection of independent and dependent variables, the Jacobian matrix is the matrix that represents this linear transformation.
Understanding Differentiation, Antidifferentiation, and Integration in Calculus
It can be computed using the partial derivatives of the independent variables. The gradient vector replaces the Jacobian matrix for a real-valued function with several variables.
Differentiation is the action of locating a derivative. Antidifferentiation is the term for the opposite process. Antidifferentiation and integration are related in the calculus fundamental theorem. The two fundamental operations of single-variable calculus are differentiation and integration.
Different Notations
Leibniz’s notation
In 1675, Gottfried Wilhelm Leibniz introduced the letters dx, dy, and dy/dx. Even today, it is frequently employed when the relationship between the dependent and independent variables in the equation y = f(x) is considered to be functional.
The variable for differentiation (in the denominator) can be specified using Leibniz’s notation, which is important for partial differentiation.
Lagrange’s notation
One of the most popular modern differentiation notations, sometimes known as prime notation, uses the prime mark and is credited to Joseph-Louis Lagrange. It denotes the derivative of a function f as f1.
The latter notation generalizes to provide the notation f(n) for the nth derivative of f, which is more convenient when discussing the derivative as a function rather than a function of itself because the Leibniz notation can be complicated in this situation.
Newton’s notation
A dot is placed over the function name in Newton’s differentiation notation, often known as the “dot notation,” to signify a time derivative.
Only derivatives with regard to time or arc length are represented using this notation. Usually, it’s applied to differential equations in differential geometry and physics. However, the dot notation is inapplicable to several independent variables and high-order derivatives (order 4 or more).
Euler’s notation
The first derivative, Df, is obtained using the differential operator D in Euler’s notation by applying it to a function f. Dnd stands for the nth derivative.
If y = f(x) is a dependent variable, the independent variable x is frequently clarified by adding the subscript x to the D.
Although when the variable x is understood, such as when this is the sole independent variable contained in the equation, this subscript is frequently left off.
For expressing and resolving linear differential equations, Euler’s notation is helpful.
Application of Derivatives in Maths
Derivatives are frequently used in mathematics. They can be used to determine a function’s maximum or minimum, the slope of a curve, or even the inflection point.
Below are a few instances where we will use the derivative. And the following sections go into great detail about each of them. The application of derivatives is most frequently found in:
- Calculating a quantity’s Rate of change
- Getting a good estimate of the value
- Finding the equation for a curve’s tangent and normal
- Identifying the point of inflection, maxima, and minima
- Assessing the increasing and decreasing functions
Application of Derivatives in Real Life
Derivatives can be used in many situations in real life. Here is a list of a few situations in which you can use derivation:
- To calculate profit and loss in the business.
- In order to measure temperature variation.
- To calculate the rate of travel, such as miles per hour, kilometers per hour, etc.
- Numerous physics equations are derived using derivatives.
- Finding the earthquake magnitude range is a favorite task in seismology research.
Conclusion
- d^2y/dx^2 is the second derivative. (dy/dx)^2 is the square of the first derivative.
- Derivatives matter in business, physics, and temperature measurement.
- Finding highs and lows in math relies on derivatives.
- The second derivative spots still points and turning points.
- Notations like Leibniz’s, Lagrange’s, Newton’s, and Euler’s help show derivatives.
- Derivatives gauge change, locate slopes, and analyze functions.
- They’re used for profits and temperature readings. Also, for physics formulas.
- Knowing derivatives matters for accurate real-world math.