A function is a mathematical relationship between two sets that are often represented by an equation. The function assigns each input a distinct output. In other words, for every input, there is only one corresponding output.
An equation is a mathematical statement that states two variables are related in a certain way. A function, on the other hand, is a set of instructions that tells a computer what to do with one or more inputs. Functions can be linear or nonlinear, and they can take any number of inputs.
Functions are simpler than equations, and they can be graphed on a coordinate plane. Equations are more complex than functions, and they cannot be graphed on a coordinate plane. Equations can also contain variables that are not used in the equation’s graph.
Let’s learn the difference in depth.
What is Function 1?
Function 1 is a mathematical function that takes one input and produces one output. It can be represented by the following equation: y=f(x).
The most basic type of function is the one-to-one function. This type of function ensures that each input has only one corresponding output. For instance, the squaring function can be graphed on a coordinate plane. Any point on the graph corresponds to a unique square value.
It’s important to note that not all functions are one-to-one. The cube root function, for example, can have multiple outputs for any given input. This is because the cube root function doesn’t guarantee that each input has a unique output.
Nevertheless, the majority of real-world functions are one-to-one, and this property can be very useful when solving problems.
For example, it’s the most important function in a company’s financial statement. It measures a company’s ability to generate profits and cash flow from its operations.
The formula for calculating a company’s function 1 is revenue minus cost of goods sold, minus administrative and selling expenses, minus interest expense, plus other income. This number is divided by the company’s net sales to get its function 1 margin.
Some real-world examples of Functions

Following are some of the examples of functions added in the table format to get a better understanding.
| Example | Elaboration |
| The Cost of Fuel | Cost depends on quantity. Gas stations can’t charge different prices for the same amount of gasoline. |
| The Cost of Taking a Taxi | The cost of a specific ride is proportional to its duration. It is not possible to have two charges with the same duration. |
| The Velocity of a Free-falling Object | The object’s fall speed is constant. Therefore, speed is a function of the object’s free fall time. |
| An ATM Machine | The requested amount depends on the disbursed amount. The machine gives exactly what you request. |
Is a function an equation?
All functions are logically equivalent to equations. However, not all equations are functions. Functions are thus a subset of equations that include expressions. Equations are used to describe them.
An equation is a mathematical equation that can be used to solve problems. A function is a set of ordered pairs (x, y) where x represents the input, y represents the output, and the function takes one input and produces one output.
A functional equation is a mathematical statement that describes the relationship between two variables. It is also known as an equation of a line or a polynomial. Functions are equations if they satisfy the following three properties:
- every variable appears at least once,
- the dependent variable depends on all the independent variables and
- there is one and only one solution for the equation.
Functional equations are equations that relate one set of variables to another. They are often used in mathematics and physics, but they can also be found in everyday life.
It is usually written as an algebraic equation, which means that it is expressed in terms of algebraic operators (such as addition, multiplication, and exponentiation). However, not all functions are expressed this way.
Are all equations considered as functions?

No, not all equations are functions. An equation is a function if and only if the equation has a unique solution for every input. For example, the equation x = 2 has two solutions, 2 and -2. However, the equation x = y + 1 has no solutions because any value of x will always be paired with the same value of y.
Frequently, a function may be represented by an equation, although not every equation is a function. Obviously, an equation might be quite simple (such as 1 + 2 = 3) and need not include any variables. Some equations represent relationships that are not functions.
In mathematics, an equation is a mathematical statement that represents a relationship between two sets of variables. Equations are considered functions because they can be graphed to show the relationships between the variables.
Although all functions are considered equations, not all equations are functions.
What equation is not a function?
A mathematical equation is a declaration of equivalence between two expressions. In most cases, the expressions are numbers or algebraic equations.
Functions are a specific type of equation in which one expression, the function, is dependent on another, the argument. However, there are equations that are not functions.
One example is the square root equation x2 = 4. While this equation has a functional solution of x = 2, it also has two non-functional solutions at x = ±2.
Vertical lines are usually not functions. One way to think of the equations as “non-functions” is to think of them as equations where at least one variable has two or more possible values.
How to Write a Function Equation
Determine your function’s value. In a sequence of functions, the value of the independent variable remains constant, allowing you to graph your results. If your function is “3x = 15,” you will know that x = 5 for all future functions in that collection.
Consider the function in terms of acquisitions. If you purchase one case of ramen, for instance, you will spend $5. However, the total amount will vary if the quantity of cases purchased is altered.
As a result, three cases of $5 ramen will cost $15, and the total price depends on the quantity ordered. It is independent of the price of each item, which remains constant. To arrange the data, you may create a graph or describe the values using a table.
Represent the function as an equation that can be used to calculate the purchase price for any extra value. This equation is the inverse of the initial function equation, which was 3x = 15.
Now that you know x = 5, you may replace the integers with variables, allowing the values to be altered according to the problem solver’s requirements. Consequently, v5 = c. This indicates that any amount multiplied by 5 will result in the cost of the desired quantity of products.
How do you determine a function?
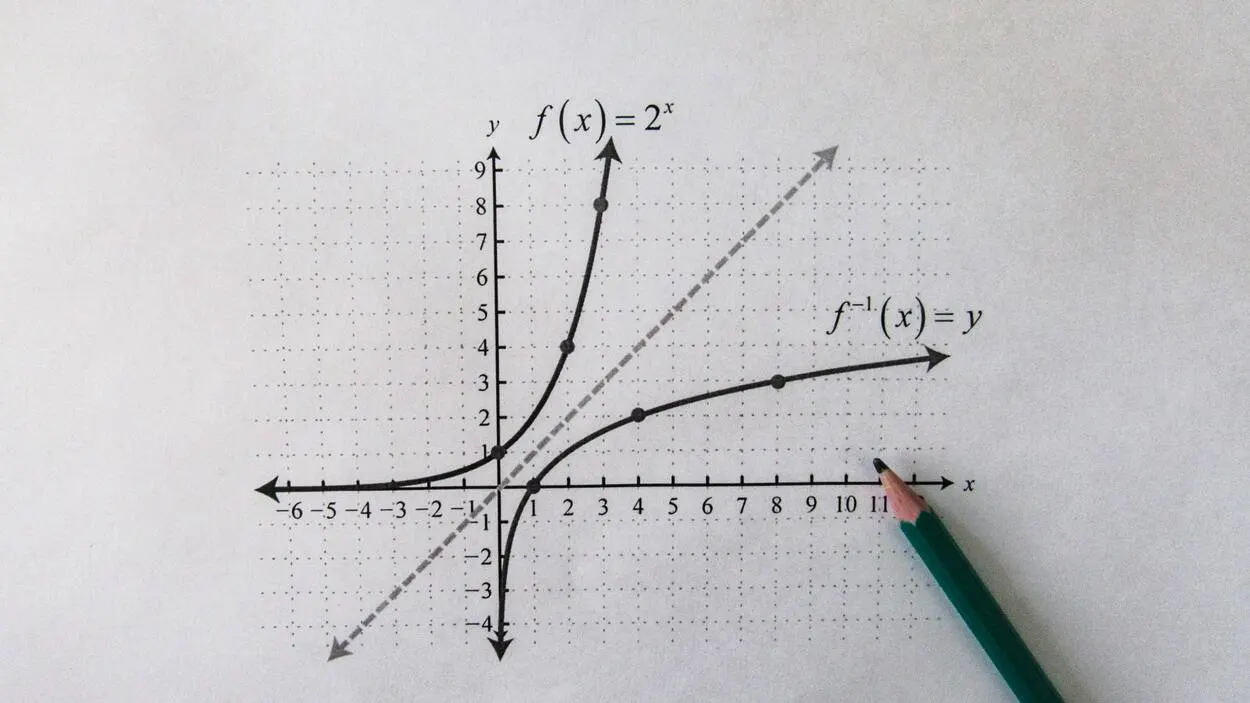
Function determination can be a daunting task for those new to calculus and even more so for those without a linear algebra background, but it is essential for understanding more complex concepts.
There are many ways to determine a function, but the most common approach is to graph the function on a coordinate plane. Once the function is plotted, its inverse can be determined by reversing the graph axes.
Using the vertical line test, it is simple to determine if a graphed relationship is a function. The relationship is a function if a vertical line crosses the graph of the relationship just once at all points.
However, if a vertical line crosses the connection more than once, it is not a function. Using the vertical line test, all lines are functional except vertical lines. Functions are not circles, squares, or other closed geometries. Instead, they are parabolic and exponential curves.
Conclusion
- Equations relate to variables. In contrast, Functions instruct computers with inputs.
- Functions can be graphed, while equations are too complex for graphs.
- Function 1 ensures one input corresponds to one output. It is important in real-world uses like financial statements.
- Real-world examples like fuel costs or taxi fares demonstrate practical function applications.
- Not all equations are functions. Each input must have a unique solution for it to be a function.
- Some equations need unique solutions, like x = 2 or x = y + 1, failing the function criteria.
- Spotting functions often involve graphing on a plane and using tests like the vertical line test.
Other Articles
- What Are the Difference Between IMAX 3D, IMAX 2D, and IMAX 70mm? (Facts Explained)
- How Are Nctzen And Czennie Related? (Explained)
- The Difference Between a Religion and a Cult (What You Need to Know)
- What’s the Difference Between an Iced and Black Tea? (Comparison)
- What’s the Difference Between Journal Writing and Journalist? (Explained)