While the chi-square test and the t-test are statistical tests employed for evaluating data, though they share distinct objectives.
A t-test is used to find out the distinction between the means of two groups, whereas a chi-square test is utilized to establish the relationship between categorical variables in each group.
To discover insights from data and reach significant findings, numerous tests are used in statistical analysis.
The chi-square test and the t-test are two often used tests. These tests have particular applications and offer perspectives on various parts of data, even though they might seem similar.
For researchers and data analysts to decide on the best analytic method according to their study objectives and data types, it is essential to comprehend the differences between a chi-square test and a t-test.
Therefore, I am going to address the key distinctions between the chi-square test and the t-test in this article while also looking at how they are used, calculated, and interpreted. Let’s get into the details!
Chi-Square Test
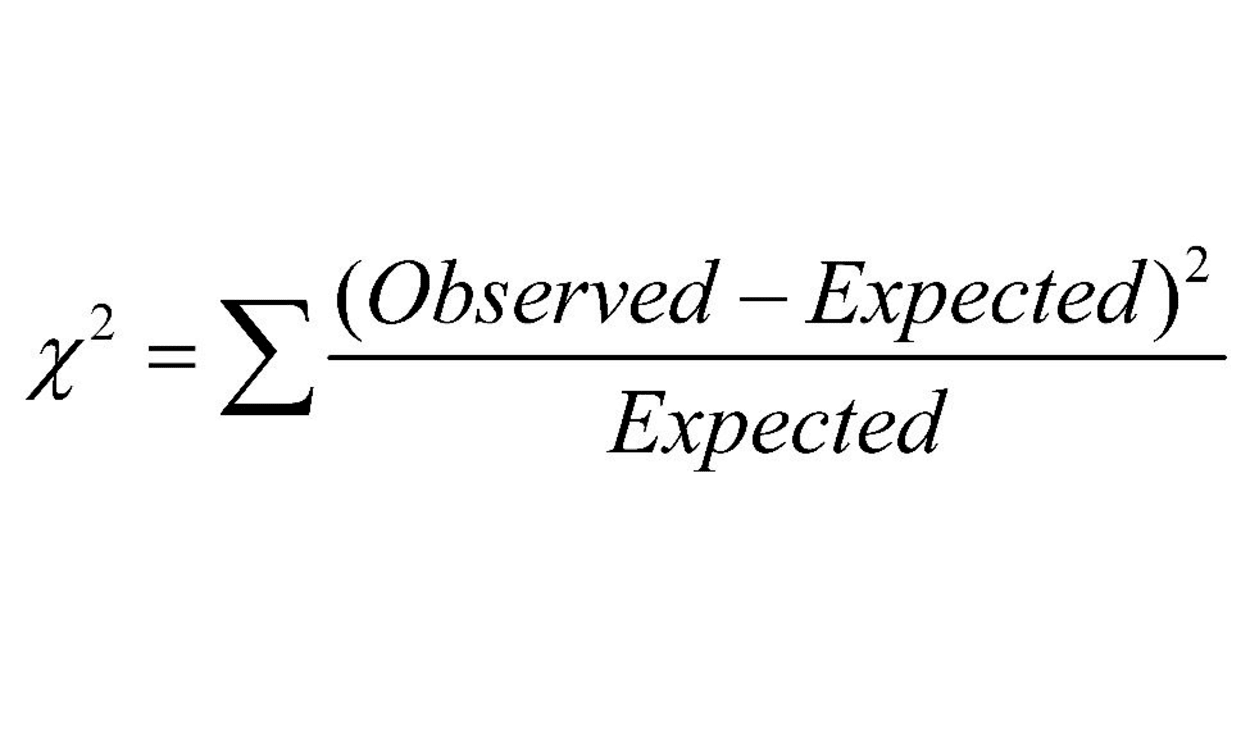
A form of statistical analysis known as the chi-square test is employed to figure out the relationship between categorical variables.
It is perfect for sorting or grouping data into multiple groups. Its uses can be seen frequently in survey results, genetic analysis, and contingency tables.
Assumptions
- Independence of observations:
Every observation is used to be autonomous of all others and undisturbed by them.
- Expected frequencies:
Each category ought to take place at least five times, guaranteeing the accuracy of the results.
Calculation and Interpretation
The disparity between the observed and expected frequencies is computed using the chi-square test, which yields the chi-square ratio.
It can measure the importance of this statistic by contrasting it to the chi-square dispersion. A strong connection between the variables is shown if the p-value is less than the selected level of relevance.
You can learn more about this topic by watching this video about the comparison of chi-square tests.
T-Test
For a comparison of the means of two groups, statisticians utilize the t-test. It is mostly used when dealing with continuous variables, like height, weight, or test results.

Researchers can assess whether there is a significant variation in means between two isolated or paired groups using the t-test.
Assumptions
- Normal distribution:
Every group’s data needs to have a normal dispersion.
- Homogeneity of variances:
The two groups getting evaluated should have about identical variances.
| Criteria | Chi-Square Test | T-Test |
| Purpose | Assess the association between categorical variables | Compare means between two groups |
| Data Type | Categorical variables | Continuous variables |
| Sample Size | No specific requirements | Sufficient sample size |
| Assumptions | Independence of observations | Normal distribution, homogeneity of var. |
| Interpretation | Significance of association | Significance of mean difference |
| Degrees of Freedom | Based on the number of categories | Based on sample size and groups |
Calculation and Interpretation
By evaluating the median, standard deviation, and proportions of samples of the two groups, the t-test generates the t statistic.
The importance of the obtained t-statistic is subsequently assessed by comparing it to the t-distribution.
A substantial variance between the means of the two groups can be detected by a p-value that is lower than the selected level of relevance.
How Do You Interpret the Results of a Chi-square Test?

A test statistic and a p-value can be obtained by the chi-square test.
More significant values indicate greater variability in the test statistic, which estimates the disparity between reported and expected values.
If there is no agreement among the variables, the p-value reflects the possibility of being given a test statistic that is similarly extreme or more intense than the observed value.
The p-value signifies that there is a substantial connection between the variables if it is lower than a preset importance level, such as 0.05.
How Do You Interpret the Results of a T-test?
A test statistic and p-value are generated by a t-test. The test statistic estimates the variance between the data set’s means; higher values suggest greater variability.
If there is no distinction in the means, the p-value reflects the chance of getting a test statistic that is equally or even more significant than the value that was seen.
There is an important impact between the means if the p-value is less than the threshold that was chosen of significance.
Can You Use a T-test for Categorical Data?
The t-test is not right for the analysis of categorical information. It was designed particularly to handle continuous variables.
A chi-square test might be preferred if you’re using qualitative data and are interested in looking at connections or differences.
What is the Effect Size in a Chi-square Test and T-test?
It is frequently helpful to gauge the influence size in both chi-square tests and t-tests alongside statistical significance.
The magnitude of the impact tells us how big or strong the connection or distinction under study is.
Cramer’s V or the Phi factor are typical effect size estimates for chi-square testing. Effect size metrics like Cohen’s d or Hedges’ g are often hired for t-tests.
Can You Perform a Chi-square Test or T-test With Multiple Groups?
Numerous group analyses can be conducted with both chi-square tests and t-tests.
When using chi-square tests, researchers can look at connections between many categorical variables by employing a chi-square test for autonomy.
Analysis of variance (ANOVA) can be employed in T-tests for comparing the means of several groups, and post hoc tests can then be utilized to discover specific category differences.
Which Test Should You Choose If You Have Both Categorical And Continuous Variables?
You will require to apply separate tests for every kind of variable if your data comprised both kinds of variables.
You can use methods like chi-square tests for categorical variables and regression analysis (like linear regression) for continuous factors to evaluate the connections between a categorical and continuous variable.
Conclusion
- Two other statistical tests that are commonly used in analyzing data are the chi-square test and the t-test.
- Although the t-test can be used for constant variables, the chi-square test works best for categorical variables.
- For dependable findings, certain requirements and hypotheses must be fulfilled for each test.
- Evaluating the test statistics and p-values is essential for understanding the outcomes of these tests.
- The right test must be chosen depending on the data’s qualities and the issue at hand.
- Researchers have more resources to make wise choices and derive accurate inferences from their data when they are mindful of the discrepancies between various tests.
- Appropriate data analysis methods can generally help in offering solid and dependable study conclusions.
Related Articles
- Differences When One Switch From Internet Speeds of 300 Mbps to 600 Mbps (Streaming Content)
- What’s The Difference Between The Falcata And Kopis? (Besides Physical Similarities)
- What Is The Performance Difference Between 256GB SSD And 512GB SSD? (Explained)
- What is the difference between sequential and event-driven programming? (Know Your Softwares)

