The terms “helix” and “spiral” may have appeared in your vocabulary while you were a student. The purpose they provide in engineering, mathematics sciences, and even biology is the cause.
A helix is a three-dimensional geometric curve, whereas a spiral is a two-dimensional one. Both terms refer to a continuing circular journey.
When discussing stairs, the distinction is obvious. Spiral staircases with a central column have this feature, although helical staircases can have more flexibility in their design.
Curves that “wind around” are referred to using the phrases spiral and helix. For instance, the terms “DNA spiral” and “DNA helix” will reveal the various configurations DNA can take in human biology.
Please continue reading to learn more about these two words and their distinctions, even though they are almost identical to one other as described.
Mathematical Curve
An unbroken line with a smooth flow and no sharp twists is referred to as a curve. It can be recognized because it bends and changes its route at least once.
Shapes that are only made up of curves are called curved shapes. An arc, circle, parabola, or other curved form can be two-dimensional. Spheres, cones, and cylinders are examples of three-dimensional objects that can have curved geometries.
A curve is created by joining many short-line segments together. If you look very closely, the lines are visible.
A closed curve’s exterior is referred to as a closed curve, whilst the inside of a closed curve is referred to as its interior. Spirals and parabolas are examples of open curves with unlimited length.
Here are the different kinds of mathematical curves:
| Types of Curves | Description |
| Upward | A curve that makes an upward turn. |
| Downward | A curve that makes a downward turn. |
| Open | It has two terminals and does not contain any space within itself. |
| Close | It encompasses space and has no endpoints. |
| Simple | It reverses course but does not cross itself in the process. It is both open and closedable. |
| Non-simple | A curve that travels over itself. |
What Is A Spiral?

A spiral in mathematics is a curve that emerges from a point and spirals outward as it rotates around the point. It belongs to the large category of whorled patterns, which also include concentric objects.
Both natural and man-made things contain spiral shapes. The first two figures below depict a spiral galaxy and a seashell, both of which are shaped like spirals. The staircase likewise has a spiral design.
Two popular 2D spirals are the golden spiral and the archimedean spiral. Let’s see how descriptive they are.
| Types of Spiral Curves | Description | Formula |
| Archimedean Spiral | The length of every radius of a concentric circle is equal to the angle measure in the standard position for every point plotted on the Archimedean spiral in the polar coordinate plane. | r = θ |
| Golden Spiral | The spiral that displays logarithmic growth is known as the golden spiral. The golden spiral widens by a factor of the Golden ratio for each quarter rotation. | φ= ≈1.618. ≈1.618. |
| 3D Spiral | A spiral is an open curve that spins around and along a line known as its axis in three dimensions. | x(t) = rcos(t), y(t) = rsin(t), z(t) = at |
The mathematical relationship between the length r of the radius vector and the vector angle q, which is made with the positive x-axis, allows for the classification of spirals.
Some common examples of a spiral object are as follows:
- The spiral curve of a watch spring
- Spiral-bound
- Spiral Notebook
Spiral Staircase
The fundamental advantage of a spiral staircase is that it uses less space than a winding staircase.
It is crucial to keep in mind that the more room you conserve typically entails a greater spiral staircase gradient.
Spiral staircases are a common choice for residential structures because of their striking aesthetic appeal. Additionally, they can be utilized as interior and exterior staircases.
Our Mole Hill project serves as an illustration of how a spiral staircase can be used effectively outside; a spiral staircase was used to provide access from the balcony to the garden without taking up any room in the garden itself.
What Is A Helix?

A helix is an angle at which all generators are intersected on the surface of a circular cylinder or a circular cone.
It is also known as a coil, which is a three-dimensional curve that revolves around a central axis. It is also known as an isocline curve, slope line, and curve of equal slope.
The characteristic that the unit tangents of helical space curves retain a constant inclination with regard to a fixed line, the helix’s axis, defines these curves. Helix has a constant curvature/torsion ratio and a circular tangent indicatrix.
There are many helices in nature. In contrast to plants like bindweed and beans that produce right-handed helices, the honeysuckle always grows in lefthanded helices.
Similar to the screw from the Python at Efteling in the picture to the right, DNA, The Double Helix, which contains our genetic code, is always righthanded.
Although the body essentially moves in a “uniform rectilinear motion” during the rotation around an axis close to the level of the heart, the heart-line roll of the Kanonen roller coaster at Liseberg also produces a right-handed helix.
Example: Helical Staircase
Although it may seem counterintuitive, a helical staircase typically requires more room than a spiral staircase, which makes it more of a focal point of the room and the entire home.
Helical stairs, in the opinion of the majority of users, look their finest in open-concept spaces, especially entrances, since they can make a modern or historic house come alive.
It should be noted that helical staircases are also frequently referred to as curved staircases. The term “helical” refers to a staircase with a helix-like shape, which is the main source of confusion because people mistakenly think all spiral staircases are the same.
Difference Between A Spiral And A Helix
A spiral is a curve that originates from some point/origin and progresses away from it uniformly, whereas a helix is characterized as a line called the axis from which every point on the curve is at an equal distance.
According to certain sources, the spiral is related to geometry, and the helix is related to mathematics. The development of a spiral and helix is perfectly explained by the examples that follow.
You’ll notice patterns in spiral development if you pay great attention to nature. For instance, trees and sunflowers have spirals because they must develop, yet safely, and are stronger when shaped like spirals.
Consider a hurricane as an illustration; it has a spiral structure and is stronger and closer to the center.
As members of nature, people too follow patterns. The DNA, which makes up our essence, is a double helix.
Our DNA is compared to a double string that has been wound twice and joined by hydrogen. Our DNA contains geometrical information, making this our genetic language.
Other Geometrical Shapes
Parabola

Each point on a parabola is equally spaced apart from both the focus, another point on the curve, and the directrix, a straight line.
The primary equation for a parabola is y=x2, and its standard form is y=ax2+bx+c. Y=x2+1 is an example of a parabola.
The rainbow and banana shapes in the yoga wheel stance resemble a parabola.
Energy can be gathered and concentrated in a single spot with the aid of parabolic reflectors. The numerous parabolic items we use on a daily basis, including satellite dishes, suspension bridges, telescopes, microphones, and spotlights, are proof of the benefits of this characteristic.
Ellipses
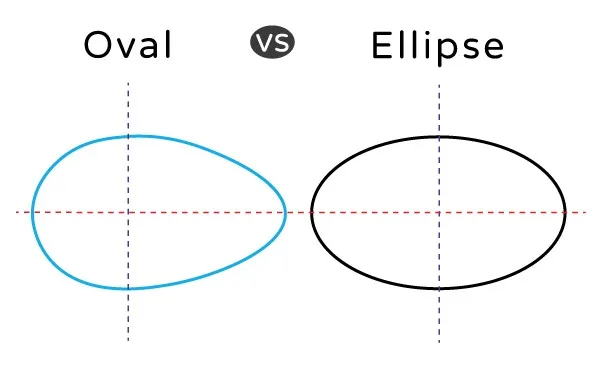
A two-dimensional shape in geometry known as an ellipse is defined along its axes; when a plane intersects a cone at an angle to the base of the cone, an ellipse is formed.
There are two foci or focal points in every ellipse; the total of the distances between any two focus points and any point on the ellipse is a fixed amount.
An ellipse has a center, a major axis, and a minor axis; an ellipse has an eccentricity value below one.
The diameter of the Major Axis is the largest. It travels along the ellipse’s widest point from one side to the other, passing through the center. Additionally, the Minor Axis has the smallest diameter.
Conclusion
- The primary distinction between a spiral and a helix is that a spiral emanates from a point and moves outward as it rounds around the point, whereas a helix is a smooth space curve.
- The tangent line of a helix has the characteristic of constantly forming a constant angle with the axis, which is a fixed line.
- Coil springs and spiral staircase railings are two examples of helices. A spiral is the location of a point that continuously moves farther away from a fixed issue while rotating around it.
- When we talk about helixes or spirals, we should also reflect on the fact that these concepts represent the expression of perfection at every level of life that exists in the cosmos and on this planet.

