Homomorphisms and isomorphisms are two frequently-used terms that often get confused. They are closely related, but there are key differences between the two concepts. To put simply, a homomorphism is a structure-preserving mapping between two algebraic structures, while isomorphism is a more specific type of homomorphism where two structures are exactly equivalent.
In this guide, we will explain exactly what homomorphisms and isomorphisms are, discuss their similarities and differences, and provide examples of each. We’ll also explain why it’s important to understand these concepts to effectively work with mathematics. By the end of this article, you will be able to confidently distinguish between Homomorphisms vs Isomorphisms. So let’s begin!
What Are Homomorphism And Isomorphism?
Homomorphism and isomorphism can be difficult to understand, and it can be easy to mix them up.
Let’s break it down. A homomorphism consists of a mapping between two groups or sets that preserves the operations within the objects. In other words, if there are two related sets and a homomorphic mapping between them that preserves the operations, then any calculation done in one set will have an equivalent answer when mapped over to the other set.
Isomorphisms are more specific types of homomorphisms that establish an equivalence between two groups or sets in which every element of one set corresponds to an element of the other set, and vice versa. Simply put, when applying an isomorphic mapping between two related structures, structure and operation are preserved such that it can be said that the two structures are indistinguishable from each other.
Key Differences Between Homomorphism And Isomorphism
These two terms are often used interchangeably, but they do have their distinct differences. Homomorphism and isomorphism denote the likeness or similarity of two abstract structures. Below, we outline the key differences between them:
- Homomorphism: This concept refers to a mapping between two algebraic structures that preserves their operations and relations. To put it simply, homomorphism denotes the similarity in structure between two sets of data or mathematical objects with the same operations and relations applied consistently throughout.
- Isomorphism: This concept relates to a mapping between two theoretical constructs that preserve their structure but not necessarily their operations and relations. Isomorphic structures have the same elements but with different names or different behavior is given to each element.
In short, homomorphisms are concerned with preserving operations and relations while isomorphisms focus on preserving structures with no specific conditions on operations and relations imposed on them.
Exploring Examples Of Homomorphism And Isomorphism
It’s easier to understand the differences between homomorphism and isomorphism when you explore examples. Here are some common examples that illustrate the key points:
Example 1: The Integer Domain
Consider the integer domain, where we can define a homomorphism f from the set of integers (Z) to the set of squares of integers (Z2):
- Z –> Z2
- n –> n2
This is an example of a homomorphism because it preserves the operation of multiplication – i.e., f(mn) = f(m)f(n).
Example 2: Graphs
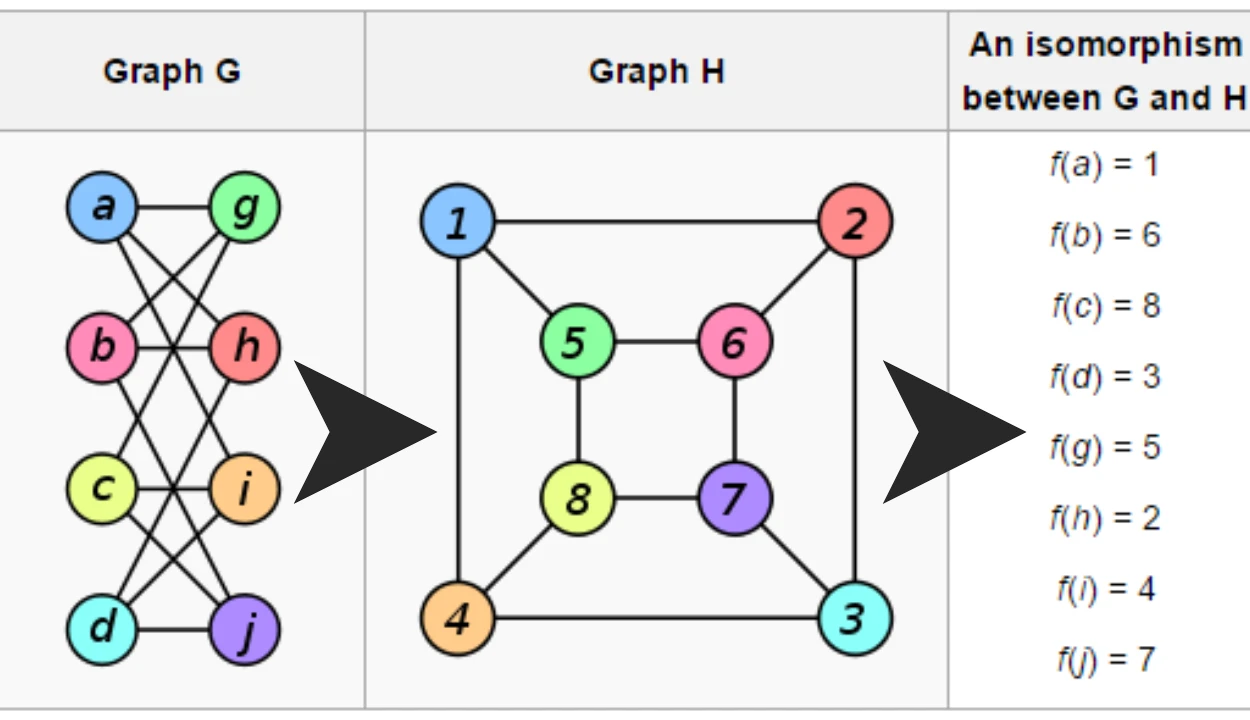
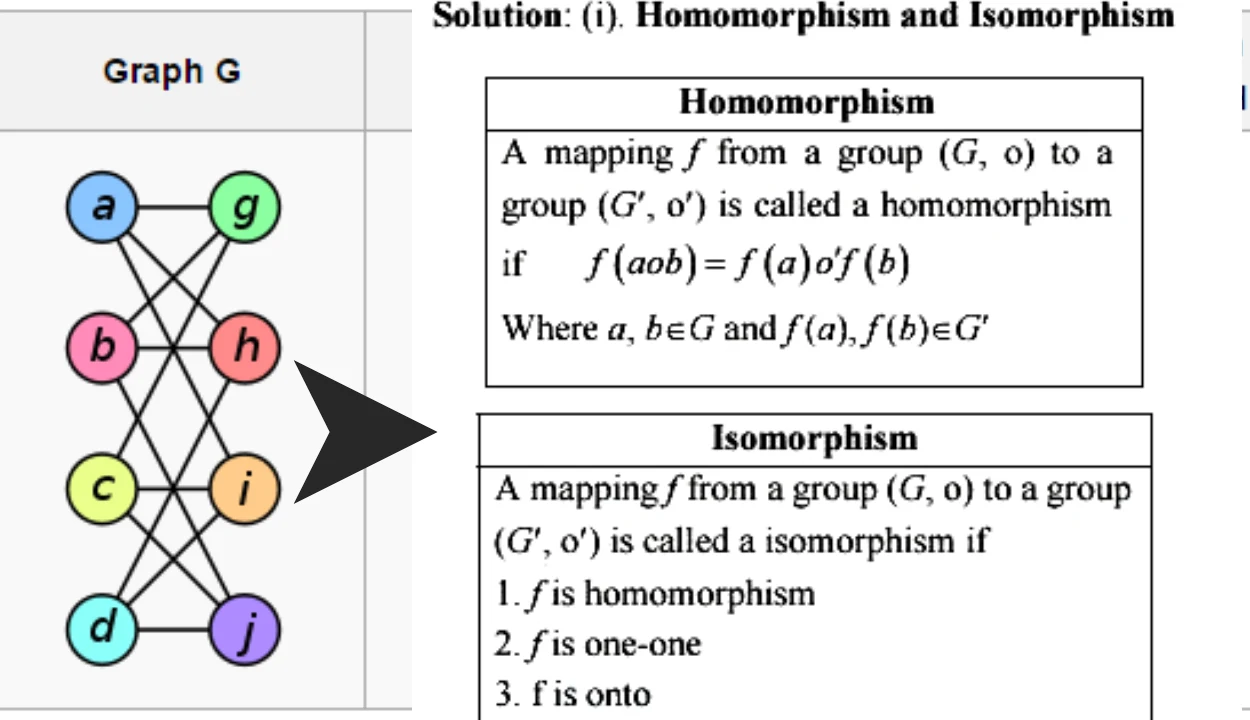
Graphs are another classic example used to explain homomorphisms and isomorphisms. A graph G with vertices V = {v1, v2, v3…} can be seen as a series of mathematical objects linked by edges. We can define two graphs G1 and G2 as homomorphic if there is a function f such that for all edges e in G1 there exists an edge e’ in G2 such that f(e) = e’. That is, after mapping each vertex in G1 to its corresponding vertex in G2 all edges remain connected in the same way.

On the other hand, two graphs G3 and G4 are isomorphic if they have identical structures – i.e., all vertices and edges are identical except for their labels. Here, there exists a one-to-one mapping f from each vertex in G3 to its corresponding vertex in G4 such that for all edges e in G3 there exists an edge e’ in G4 such that f(e)
The Implications Of Homomorphism In Modern Mathematics
Homomorphism is one of the most important concepts in modern mathematics, as it can be used to define mathematical relationships in abstract terms. To start, let’s look at the two terms commonly used when discussing homomorphism: homomorphism and isomorphism.
| Topic | Implications of Homomorphism in Modern Mathematics |
|---|---|
| Algebraic Structures | Homomorphisms can be defined between various algebraic structures such as groups, rings, fields, and vector spaces. |
| Simplification | Homomorphisms can be used to simplify complicated mathematical expressions and structures by mapping them to simpler structures. |
| Isomorphism | An isomorphism is a bijective homomorphism, which implies that two structures are essentially the same. Homomorphisms can be used to determine if two structures are isomorphic. |
| Kernel and Image | Homomorphisms have a kernel and image, which are important concepts in modern mathematics. The kernel is the set of elements that map to the identity element of the target structure, while the image is the set of elements in the target structure that are mapped to by homomorphism. |
| Applications | Homomorphisms have applications in various fields such as cryptography, computer science, and physics. For example, homomorphisms can be used to encrypt and decrypt data in cryptography, and in physics, homomorphisms can be used to describe symmetry operations in particles and crystals. |
Understanding homomorphism and its implications for modern mathematics can help us better understand how we can use mathematics to make sense of our world and effectively solve difficult problems in numerous areas.
How to Apply Isomorphic Principles To Computer Science Problems
Isomorphic principles can be applied to computer science problems in a variety of ways. For example, when designing a website, programmers can use isomorphic techniques to map images and objects in the same way across different pages. This allows for the efficient reuse of code and facilitates site navigation.
Another way isomorphism can be applied is by using abstraction layers to make data structures more universal and easily transferable between different languages. By doing this, the same data can be accessed from any language, making software easier to develop, maintain and scale.
Finally, isomorphic principles can also be used for algorithm optimization. By choosing the right mapping for an algorithm problem, it can often be solved more quickly without having to use additional resources or processing power. This is especially useful for large-scale computational problems that are too complex for a single machine alone.
Understanding The Differences
Now that you have a better understanding of homomorphism and isomorphism, you can summarize their differences. Homomorphism is a mapping between two algebraic structures that preserves the operations of one structure in the other. Isomorphism, on the other hand, is a bijective mapping between two mathematical objects (such as algebraic structures) that preserves both the operations and relationships between elements in one object to the other. Check this video out for even more details:
In short:
- Homomorphism is a mapping between two algebraic structures that preserves the operations of one structure in the other.
- Isomorphism is a bijective mapping between two mathematical objects (such as algebraic structures) that preserves both the operations and relationships between elements in one object to the other.
FAQs
What is homomorphism in modern mathematics?
Homomorphism is a structure-preserving map between two algebraic structures. It is a key concept in modern mathematics, used to simplify complicated mathematical expressions and structures.
What algebraic structures can homomorphisms be defined between?
Homomorphisms can be defined between various algebraic structures such as groups, rings, fields, and vector spaces.
How are homomorphisms used to simplify mathematical expressions and structures?
Homomorphisms map complicated structures to simpler structures, which can aid in the understanding and analysis of those structures.
What is isomorphism in modern mathematics?
An isomorphism is a bijective homomorphism, which implies that two structures are essentially the same. Homomorphisms can be used to determine if two structures are isomorphic.
What are the kernel and image of a homomorphism?
Homomorphisms have a kernel and image, which are important concepts in modern mathematics. The kernel is the set of elements that map to the identity element of the target structure, while the image is the set of elements in the target structure that are mapped to by homomorphism.
Conclusion
- In conclusion, homomorphism and isomorphism are two distinct yet related terms in mathematics.
- A homomorphism is an equation that preserves the structure of a given set while an isomorphism is an equation that preserves both the structure and the content of a set.
- Homomorphisms are useful in understanding, interpreting, and generalizing sets and often serve as the basis for creating algorithms in computing, while isomorphisms are useful for demonstrating equivalencies between groups.
- Understanding the difference between the two, as well as their individual benefits, is essential to properly applying their use in various fields.
Other Articles
- What Is The Difference Between The HC-06 And Others? (Get To Know)
- What’s The Difference Between A VPN And A DNS Cloak? (Get To Know)
- What Is The Difference Between char* And char[]? (Understand)
- What’s The Difference Between “Make somebody do something” And “Making somebody do something”? (Learn English)