Math is all about formulas and calculations. Math study can be split into branches like algebra, arithmetic, geometry, etc.
Geometry is about shapes, from simple circles and squares to complicated ones like rhombuses and trapezoids. To study these shapes, you also need formulas.
2 pi r is the formula used to calculate the circle’s circumference, while pi r squared is used to calculate the area of a process. In a circle of radius, 2 pi r is the circumference, and pi r squared is the area.
Let’s dive into the details of these two formulas.
2 Pi r: What Does It Mean?
2 pi r means to multiply 2 with pi and then multiply the answer by the circle’s radius. It’s used to calculate the circumference of a circle.
You have to calculate the circumference of a circle. Since Pi is a ratio, it’s included. Since 2r = the diameter, the number 2 and the value of r are included. Therefore, Pi multiplied by 2 times r equals circumference divided by diameter, equating to the circumference.
How was Pi derived?
Long ago, people discovered that travelling around a circle takes approximately three times as long as going straight across. The ancient Egyptians and Babylonians were more successful with approximations 3 and 1/8.
By sandwiching a circle between two polygons and increasing the number of sides on each, Archimedes could obtain a remarkably accurate approximation.
In 1706, mathematician William Jones assigned this constant the Greek letter. This was not popularized until roughly 1736, when Leonhard Euler used it.
Pi r Squared: What Does It Mean?
A circle’s area is calculated using “pi r squared.”
Pi r squared means multiplying pi times the radius and multiplying this result by the radius again. In this way, you’ll have the area of the circle. There are two ways to write this equation: pie * r 2 or * Π* r 2. You have to determine a circle’s radius first, which is half of the distance of a straight line crossing its centre.

Here are the definitions of terms for Pi r Squared:
| Terms | Definition |
| Pi | A value that approximately equals 3.14 |
| r | Radius of a circle |
| Squared | A value multiplied by itself |
Know The Difference Between 2 Pi r And Pi r Squared
Here are a few differences between both formulas.
- 2 pi r is the formula for the circle’s circumference, whereas pi r squared is the formula for the area of the circle.
- The unit of 2 pi r is inches or meters while that of pi r squared is square inches or square meter.
- Another difference is how many times the radius is squared. For example, you’ve got 2 x 2 equals four times the radius cubed. In comparison, the radius of pi r squared is nine times the radius of the second power.
Is 2 Pi r The Same As The Pi r 2?
2 pi r and pi r squared are not the same things.
2 pi r is the circumference of the circle. It means you calculate only the outer line of a circle through it. On the other hand, the pi r square is the area of a circle that refers to the whole area inside the circumference of a circle. So, they are different.
What Is 2 Pi r Equal To?
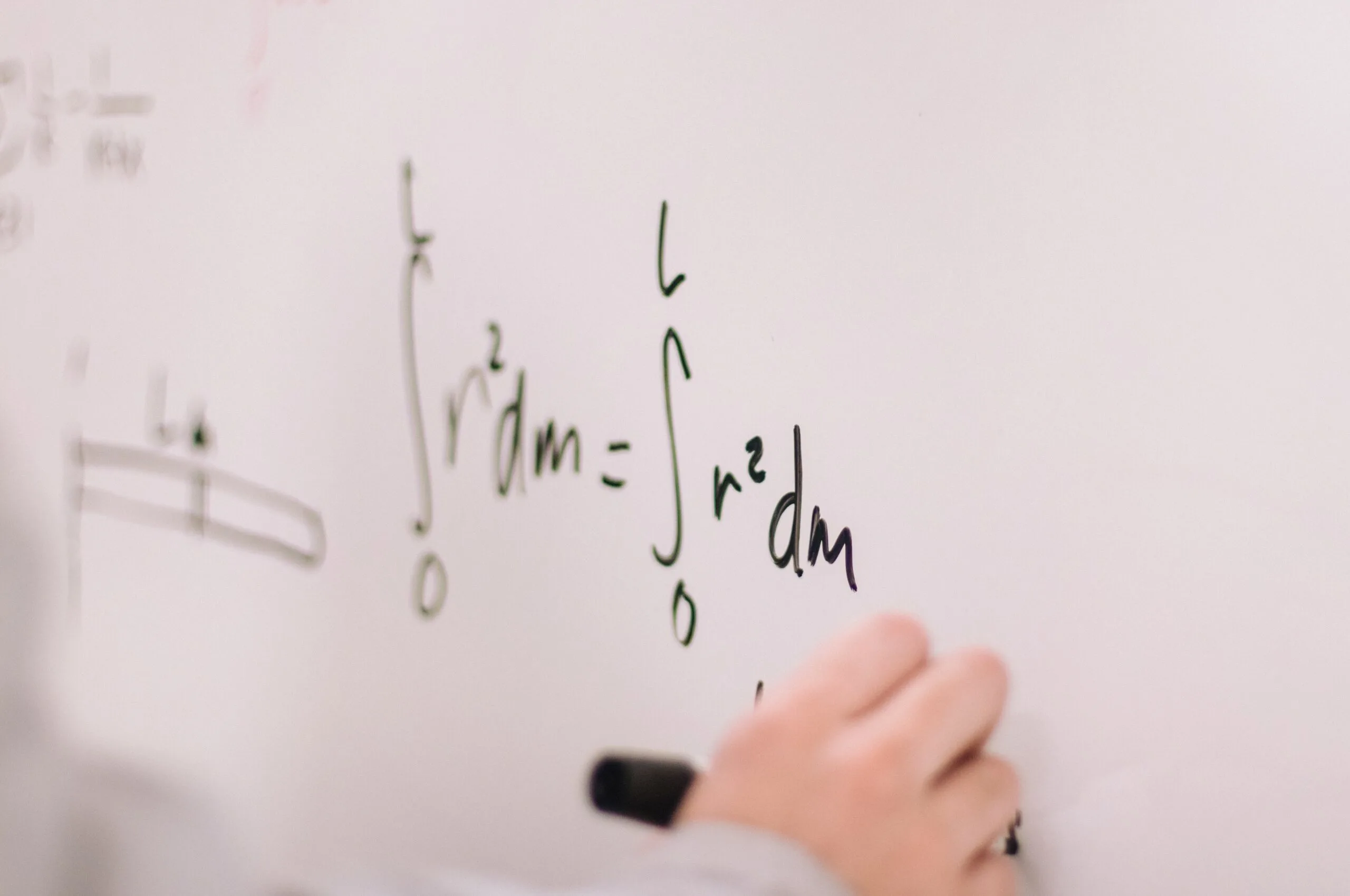
2 pi r is equal to the circumference of a circle.
You can calculate the circumference of a circle using this formula, given that the radius of that circle is r. The radius of the circle is equal to half of its diameter.
Why Is The Area Of A Circle Pi r squared?
There is a geometric justification for why the area of a circle is pi r squared.
Pi is the ratio between a circle’s circumference and its diameter, so the circumference of a circle is pi times its diameter or 2 pi times its radius. When you can cut a circle up and re-arrange it, it looks like a parallelogram (with height r, base pi times r), whose area is pi times the square of the radius.
It would be even better to divide the circle into more than eight slices. The approximating parallelograms get closer and closer to the circle’s area by slicing the circle into more and more rectangles. That’s why the area of a circle is pi r squared.
Here is a short video clip explaining a few things about the circumference and the area of a circle.
What Is The Exact Value Of Pi?
Pi is approximately 3.14. There’s a formula that tells you precisely what pi is.
Unfortunately, there are many issues where – we don’t have unlimited time to write down an infinite number of digits. It’s nearly impossible to write down that precise value since the numbers go on forever. There is only one way to express π ‘s value – a rational approximation of 3.142.
How Close Can You Get To The Square Root Of Pi?
You can’t do anything more than having it exact.
You can get into a decimal expansion depending on what kind of device you’re using, how much time you’ve got, and how good your algorithm is. It’s up to you how far you want to go.
Who Discovered Pi?
Pi was invented by a British mathematician named William Jones in 1706.
It’s the ratio of the circumference of a circle to its diameter d. In mathematics, pi can be found in lengths of arcs or other curves, areas of ellipses, sectors, and other curved surfaces, and volumes of solids.
It’s also used in various formulas in physics and engineering to describe periodic phenomena like pendulum movements, pulsating strings, and alternating electric currents.

Final Takeaway
- Geometry relies on formulas, and circles involve crucial formulas like 2πr and πr².
- 2πr calculates a circle’s circumference. πr² computes its area.
- π, originally approximated by ancient civilizations, represents the ratio of a circle’s circumference to its diameter.
- For circumference calculation, 2πr multiplies π by the circle’s diameter or twice its radius.
- πr² multiplies π by the radius squared to determine the circle’s area.
- These formulas have distinct purposes. 2πr measures the outer line of a circle, and πr² calculates its entire internal area.
- Pi’s infinite decimal value is approximately 3.14. It is pivotal in geometry and various scientific fields.
- William Jones introduced π in 1706. Since then, it has been utilized in equations. It describes curved surfaces and periodic phenomena in physics and engineering.

